Unlocking the Secrets of Secret Sharing

In this blog post, we’re going to dive into the world of secret sharing. You might be wondering, what the heck is secret sharing? Well, it’s a way to protect sensitive information by dividing it up and giving pieces to different people. But, only certain group of people can put the pieces back together to reveal the secret

Idea

The idea is simple. Let’s say we have a secret message that we want to share with a group of people. We can divide the message into pieces and give each piece to a different person. Then, only if we have a certain number of pieces, we can put them back together to reveal the secret message.

Let’s begin with a simple example. Imagine a situation that you want to share with your friends a very secret information that they will only be able to decipher on the basis of all its parts.

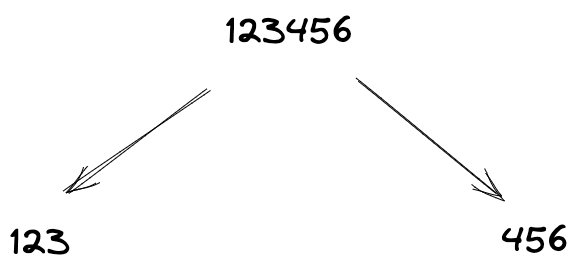
Figure 1: The idea of dividing secrets

In the example above, we have secret 123456 divided into 2 shares: 123 and 456. Each piece of a secret is called a share. We can give each share to a different person. Then, if we have both shares, we can put them back together to reveal the secret.

The problem is, if we only have one share, we cannot reveal the secret. We need at least two shares to put them back together.

Unfortunately, our solution has a number of flaws. Please note, that our 6 digit long secret can be guessed at most in a million tries, but each share of the secret has some information about it. By knowing the first part of the 123 secret, we’ll have an easier time figuring out the rest. This means that we can only have 1000 possible secrets. This is not a lot. We can easily brute force the secret by trying all 1000 possible secrets.

We need to somehow eliminate the possibility of guessing the secret based on the shares we have and make sure that the shares are not giving away any information about the secret.

Randomness

Random numbers can help us solve this problem. Let’s generate a random number between 0 and 1000000, for example, 372641. Now let’s add this number to our secret: 123456 + 372641 = 496097, we got a new random secret.

Now we can give a random number to one person, and the random secret to another person:

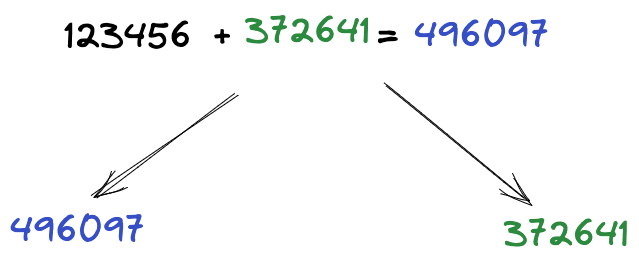
Figure 2: Divide secret into two shares with a random number

Now, there is no way to guess the original secret based on the shares we have. To reveal the secret, we need to subtract the random number from the random secret: 496097 - 372641 = 123456.

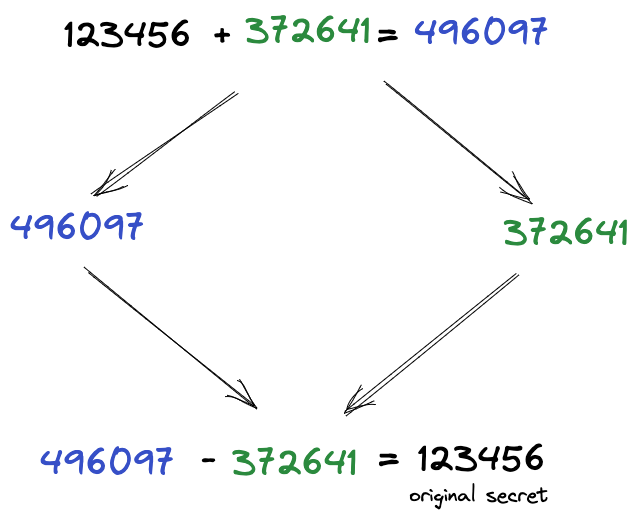
Figure 3: Reveal the secret by subtracting the random number from the random secret

Remember, we can only reveal the secret if we have both shares. If we only have one share, we cannot reveal the secret.

The method presented above is called additive secret sharing. It’s a very simple method, but it has a number of flaws. In order to reveal the secret, we need n shares, which is a major disadvantage. If k is less than n, we cannot divide the secret into n shares and reveal the secret with k shares.

Threshold secret sharing

Threshold secret sharing is a method that allows us to divide the secret into more shares. We can divide the secret into any number of shares, and we can also specify the number of shares we need to reveal the secret.

For example, we can divide the secret into 5 shares, and we can specify that we need at least 3 shares to reveal the secret:

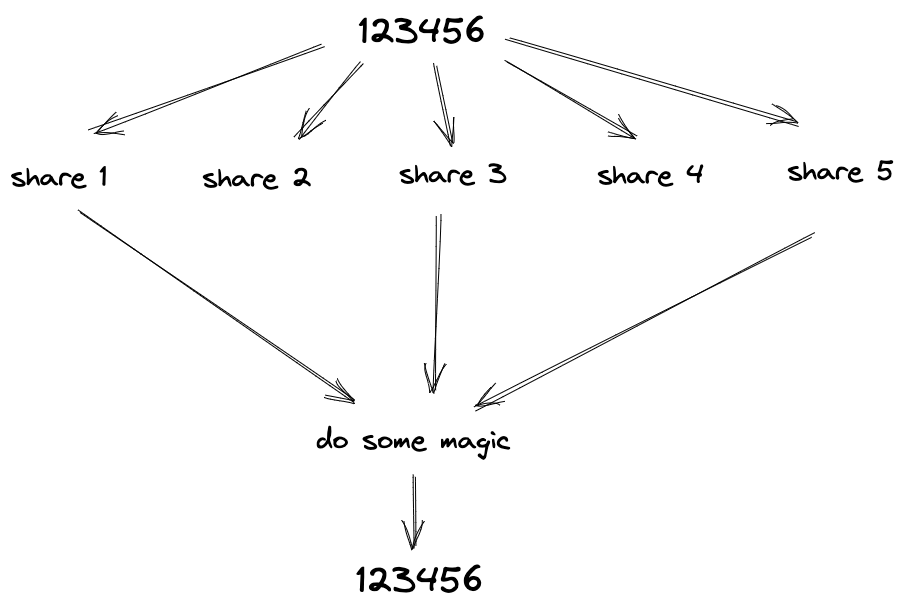
Figure 4: Divide the secret into 5 shares and specify that we need at least 3 shares to reveal the secret

This means that we can give 3 random shares to 3 different people, and we can reveal the secret.

In general, threshold secret sharing divides the secret into n shares, and we can reveal the secret if we have at least k shares, where k is less than n.

One of the most popular threshold secret sharing methods is Shamir’s secret sharing.

Shamir’s Secret Sharing

In 1979, Adi Shamir presented a method of threshold secret sharing. The method is based on the idea of polynomial interpolation.

Polynomial interpolation

Polynomial interpolation is a method of finding a polynomial function that passes through a given set of points. For example, let’s say we have a set of points: (1, 2), (2, 3), (3, 5). We can find a polynomial function that passes through these points. The function will look like this: f(x) = 2x + 1:

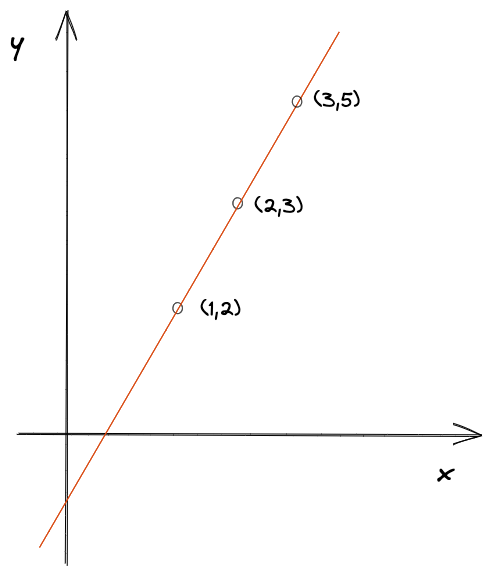
Figure 5: Find a polynomial function that passes through a given set of points

In the example above, we have got a very simple linear function. But, we can also find a polynomial function that passes through a given set of points. For example, let’s say we have a set of points: (1, 2), (2, 3), (3, 5), (4, 8). We can find a polynomial function that passes through these points. The function will look like this: f(x) = 2x^2 + 3x + 1.

To interpolate a polynomial function, we need to know at least n points, where n is the degree of the polynomial function. Using numerical methods such as Lagrange interpolation, we can find a polynomial function that passes through a given set of points. So to find a linear function, we need at least 2 points and to find a quadratic function, we need at least 3 points.

Algorithm idea

The Shamir’s secret sharing It is a method for dividing a secret into multiple shares in such a way that any subset of a certain number of shares (called the “threshold”) can be used to reconstruct the original secret, while any subset of fewer shares provides no information about the secret. Algorithm divides the secret into n shares, and we can reveal the secret if we have at least k shares (k is a “threshold”), where k is less than n.

The idea is extremely simple. Shamir expanded the idea of the interpolation, geometrically by imaging the original secret as a point on a plane (on the y-axis). Then, he placed n shares as a points along as secret curve:

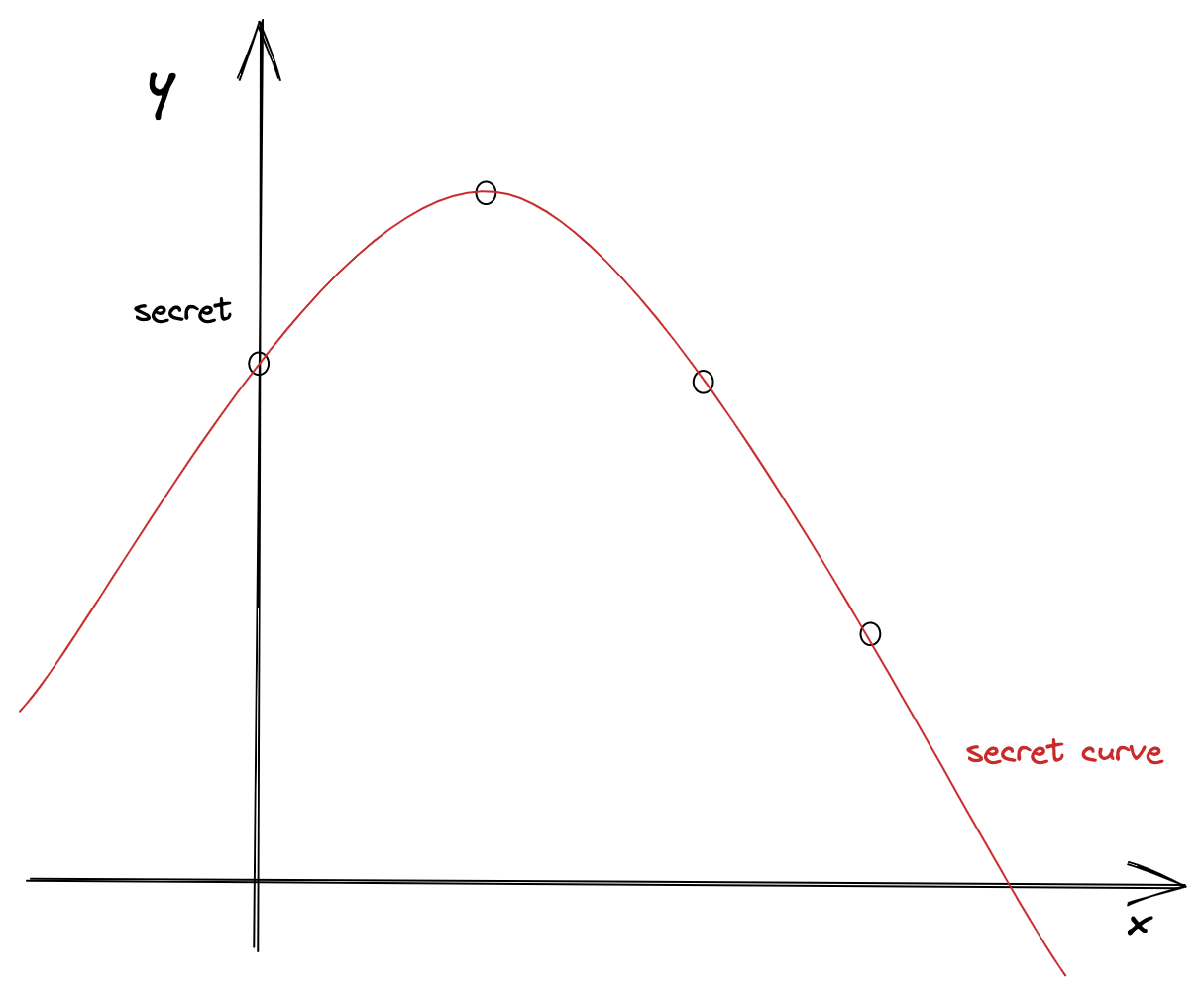
Figure 6: Divide the secret into n shares and place them along the secret curve

The secret is a point on the y-axis, and the shares are points that are placed along the secret curve.

As shown in the example above, there are three shares along the quadratic secret curve. We can reveal the secret if we have at least 3 shares. If we have 2 shares, we cannot reveal the secret.

How it works?

Here is a step-by-step explanation of how it works:

1. First, we need to define a “threshold” value k, which represents the minimum number of shares required to reconstruct the secret.
2. Generate a random polynomial of degree k-1 with the secret as the y-intercept.
3. Evaluate the polynomial at n different points, where n is the total number of shares desired. The results of the evaluations are the n shares.
4. Give the shares to n different people. Each share is a pair (x, f(x)) where x is the point of evaluation, and f(x) is the result of the evaluation.
5. To reconstruct the secret, any k of the shares can be used to interpolate the original polynomial using Lagrange interpolation. The y-intercept (f(0)) of this polynomial will be the original secret.

Example of the algorithm:

• Let k = 3, n = 5 and secret value will be secret=5, so to reconstruct the secret, we need at least 3 od 5 shares.
• Generate a random polynomial of degree 2 with the secret as the y-intercept f(0) = 5. For example, the polynomial is f(x) = 3x^2 + 2x + 5.
• Evaluate f(x) for x=1, x=2, x=3, x=4 and x=5. The results are the shares: f(1)=10, f(2)=21, f(3)=38, f(4)=61 and f(5)=90.
• Create a set of shares: S = {(1, 10), (2, 21), (3, 38), (4, 61), (5, 90)}, the original secret is a point (0, 5).
• To reveal the secret, we need at least 3 shares. For example, we can use shares (1, 10), (2, 21) and (3, 38). We can use any k shares to reveal the secret.
• Now, using any interpolation method (for example, Lagrange interpolation), we can find the original polynomial f(x) = 3x^2 + 2x + 5.
• The original secret is the y-intercept of the polynomial f(0) = 5.

Figure 7: Example of Shamir’s secret sharing

It’s important to note that the secret is not stored in any of the shares. Each share only contains a point on the polynomial, and without the threshold number of shares, it is computationally infeasible to determine the polynomial and thus the secret.

Security

Shamir’s secret sharing is a very secure method, based on mathematical properties of polynomials. The secret is not stored in any of the shares, and without the threshold number of shares, it is computationally infeasible to determine the polynomial and thus the secret.

The security of the system comes from the fact that, even if an attacker obtains some shares, they will not be able to reconstruct the secret without obtaining enough shares to meet the threshold set by the administrator. Additionally, the algorithm can be made more secure by using large prime numbers as the basis for the polynomials used in the scheme.